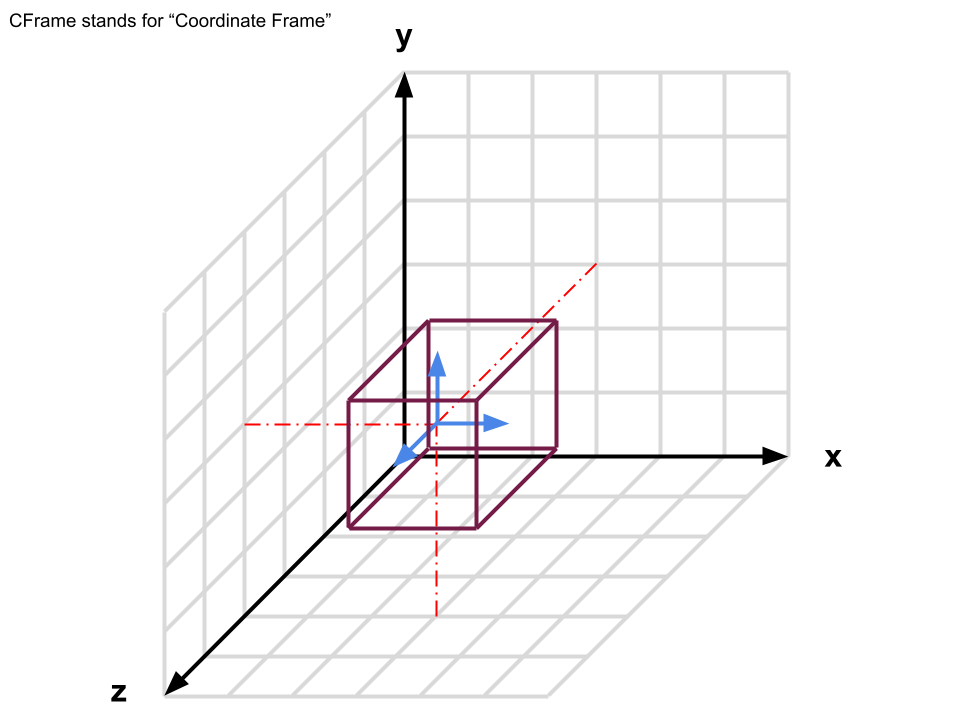
Linear algebra is very important in many video games. Roblox is a popular game amongst younger children. The "experiences" or games in Roblox simulate 3D space. Players exist in that 3D space. Linear algebra is great at representating both their position and direction.
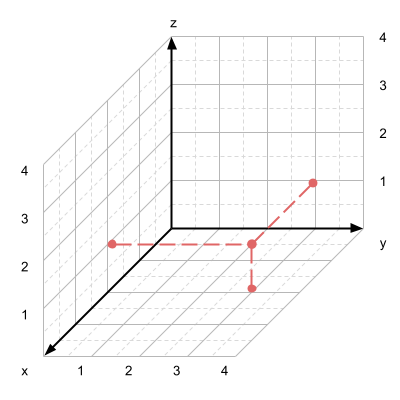
The visual above can express the position of an object in 3-dimensional space. The point can be expressed as a Cartesian coordinate.
\[ (2, 3, 1) \]We can also express this as a vector.
\[ \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} \]What are the advantages of using a vector as opposed to a coordinate? Well, we can perform operations on coordinates and find things such as their magnitude, angle with respect to a coordinate axis, etc.
As an example, vector operations can be used to find the length of the vector above.
\[ \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} = 4 + 9 + 1 = 14 \]The length squared of a vector is equal to the dot product of the vector with itself. This means the length of this vector in particular is \(\sqrt{14}\). Another way to say this is that the distance between the origin and the head of the vector is \(\sqrt{14}\) units.
In Roblox, there are two main vectors used for players and objects. One for their position and one for their direction.

Orientation can be thought of as direction.
For simplicity, we will investigate this in 2-dimensional space. However, note that this can easily be translated to 3-dimensions (or higher if need be).
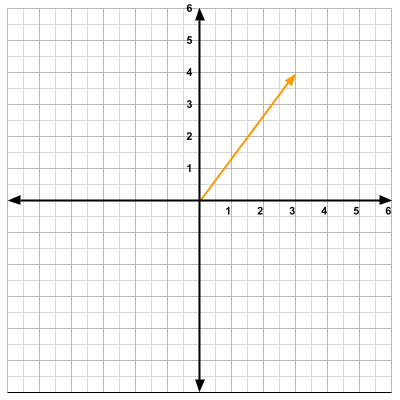
Say we have some vector in 2-dimensional space. This vector will represent a player's position.
For the direction, we can add append a different vector to the head of the position vector. The direction vector will be a unit vector.
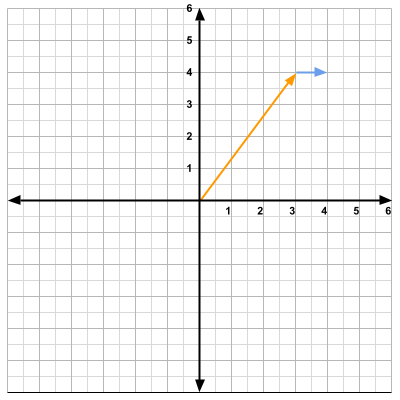
We will denote the position vector as \(\vec{p}\) and the direction vector as \(\vec{d}\). From the visuals, we see that
\[\vec{p}= \begin{bmatrix} 3 \\ 4 \end{bmatrix} \qquad\vec{d}= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]If we would like to move the player 1 unit to the right, all we have to do is add the position vector and the direction vector.
\[\vec{p}+\vec{d}= \begin{bmatrix} 3 \\ 4 \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 4 \\ 4 \end{bmatrix} \]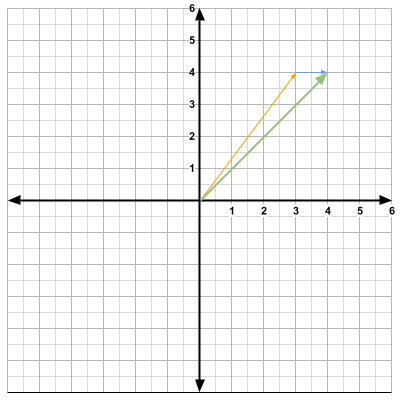
The position vector \(\vec{p}\) is now
\[ \vec{p} = \begin{bmatrix} 4 \\ 4 \end{bmatrix} \]We take the direction vector and again, append it to the head of the position vector.
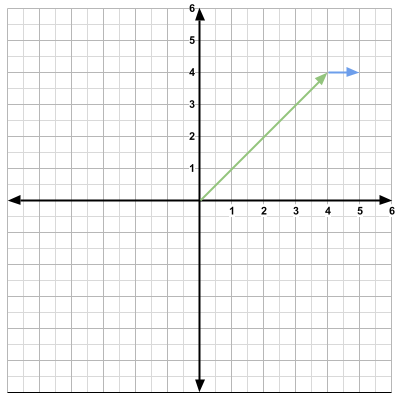
How do we change the direction? We use a rotation matrix.
\[ \textbf{R}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \]Let's do a 90 degree rotation.
\[ 90° = \frac{\pi}{2} \] \[ \textbf{R}\left(\frac{\pi}{2}\right) = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \]All we have to do is multiply the 90 degree rotation matrix with the direction vector.
\[ \textbf{R}\left(\frac{\pi}{2}\right)d = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]The direction vector is now
\[ \vec{d} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]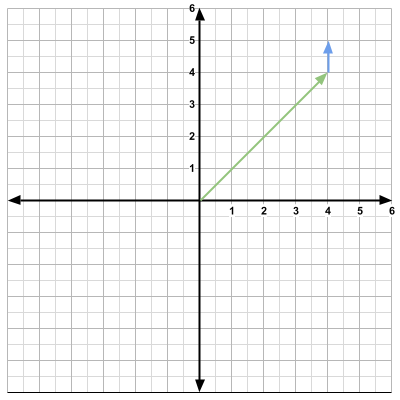
The player is now facing north. Note that we could have chosen any angle for the rotation. For instance, the player would be facing the northeast direction had we chosen 45 degrees. Now if we would like to move in that direction, we just add the direction vector to the position vector once again.
\[ \vec{p} + \vec{d}= \begin{bmatrix} 4 \\ 4 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 5 \end{bmatrix} \]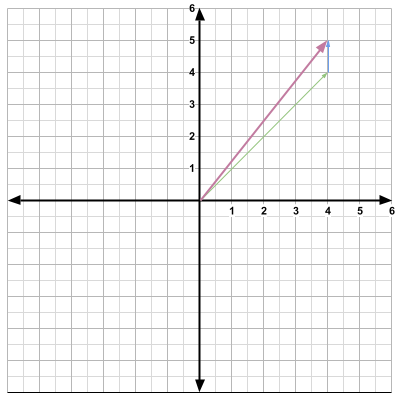
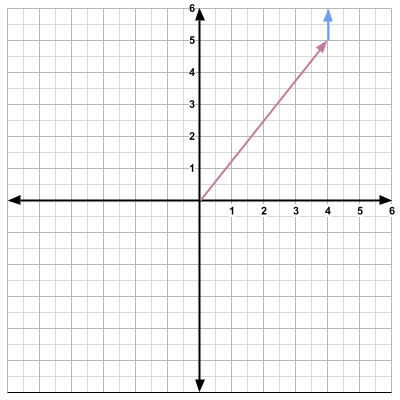
and now
\[\vec{p}= \begin{bmatrix} 4 \\ 5 \end{bmatrix} \]Now that we have done this in 2-dimensions, I bet you can imagine how easy it is to transfer this to 3-dimensional space. Additionally, multiple vectors can be displayed at once.
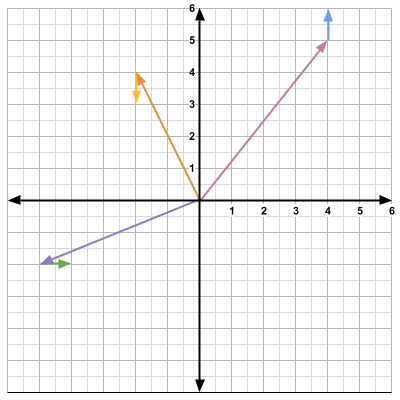
CFrames