Given two vectors \(a = (a_{1}, a_{2}, \ldots, a_{n})\) and \(b = (b_{1}, b_{2}, \ldots, b_{n})\), the dot product of \(a\) and \(b\) is
\[ a \cdot b = a_{1}b_{1} + a_{2}b_{2} + \cdots + a_{n}b_{n} \]The dot product of these two vectors can also be expressed as
\[ a \cdot b = ||a|| \ ||b|| \cos{\theta} \] where \(\theta\) is the angle between \(a\) and \(b\)This can be proved using the law of cosines.
\[ c^{2} = a^{2} + b^{2} -2ab\cos\gamma \]
Computational Proof:
The following visual will be used to aid in the proof.
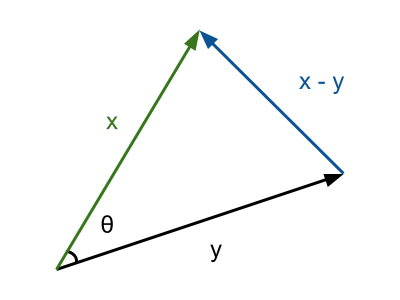
Let \(x\) and \(y\) be two vectors and \(\theta\) be the angle between them.
Applying the law of cosines, we start with the following equation.
\[ ||x-y||^{2} = ||x||^{2} + ||y||^{2} - 2||x|| \ ||y||\cos\theta \]Rearranging the LHS,
\[ \begin{align} ||x-y||^{2} &= (x-y)^{T}(x-y) \\ &= (x^{T}-y^{T})(x-y) \\ &= x^{T}x - x^{T}y - y^{T}x + y^{T}y \\ &= ||x||^{2} + ||y||^{2} - 2x^{T}y \end{align} \]Now we will use this to perform a substitution with the first equation.
\[ ||x||^{2} + ||y||^{2} - 2||x|| \ ||y||\cos\theta = ||x||^{2} + ||y||^{2} - 2x^{T}y \] \[ 2||x|| \ ||y||\cos\theta = 2x^{T}y \] \[ ||x|| \ ||y||\cos\theta = x^{T}y \]Recall \(x^{T}y = x \cdot y\).
Therefore
\[ x\cdot y = ||x|| \ ||y||\cos\theta \]Q.E.D.
The formula for the dot product leads directly to an important inequality in much of mathematics.
Cauchy-Schwarz Inequality
\[ a\cdot b \leq ||a|| \ ||b|| \]This inequality is relatively easy to prove.
Proof:
Let \(a\) and \(b\) be two vectors.
\[ |a\cdot b| = ||a|| \ ||b||\cos\theta \] \[ -1 \leq \cos\theta \leq 1 \] \[ |\cos\theta| \leq 1 \]This imples
\[ |a\cdot b| = ||a|| \ ||b|| |\cos\theta| \leq ||a|| \ ||b|| \]Thus
\[ |a\cdot b| = ||a|| \ ||b|| \]Q.E.D.
Linear combinations are pretty easy to understand. Let's say we have two vectors \(\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\) and \(\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\).
Linear combinations of these vectors are obtained by computing \[ c\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + d\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\] for real numbers \(c\) and \(d\).
For instance, if we let \(c=2\) and \(d=1\), we find that \[ 2\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix} + \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \\ 7 \end{bmatrix} \] is a linear combination of our two initial vectors. The concept of linear combinations is very important in linear algebra.
This rule serves as a useful interpretation of vector addition.
Example:
\[ v = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \qquad w = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \] \[ v + w = \begin{bmatrix} 1 \\ 2 \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 3 \end{bmatrix} \]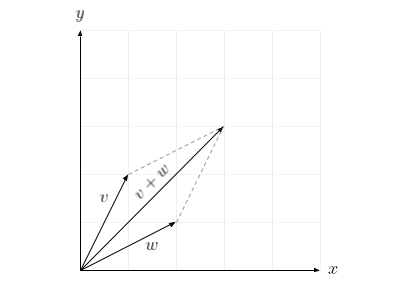
There are several different ways that matrix multiplication can be perceived.
Matrix multiplication is associative. Matrix multiplication can be thought of as a composition of linear transformations. Compositions are associative. For example, think of functions.
\[ ((f \circ g) \circ h)(x) = (f \circ g)(h(x)) = f(g(h(x))) \]while
\[ (f \circ (g \circ h))(x) = f((g \circ h)(x)) = f(g(h(x))) \]Matrix multiplication is (often) not commutative. Why? Again, we can think of it in terms of compositions. Function compositions are not commutative.
\[ (f \circ g)(x) = f(g(x)) \quad \neq \quad (g \circ f)(x) = g(f(x)) \]Despite this fact, there are instances where the multiplication of specific matrices actually happens to be commutative. Two matrices \(\textbf{A}\) and \(\textbf{B}\) are said to commute if
\[ \textbf{A}\textbf{B} = \textbf{B}\textbf{A} \]The commutator
\[ [\textbf{A}, \textbf{B}] = \textbf{A}\textbf{B} - \textbf{B}\textbf{A} \]The commutator of two matrices is the zero matrix if and only if the two matrices commute.
Vectors are linearly independent if they cannot be expressed as a combination of each other.
There are four fundamental subspaces. For a matrix \(\textbf{A}\), those subspaces are the column space, denoted \(C(\textbf{A})\), the row space, denoted \(R(\textbf{A})\), the nullspace, denoted \(N(\textbf{A})\), and the nullspace of \(\textbf{A}^{T}\), sometimes called the left nullspace which is denoted \(N(\textbf{A}^{T})\). These subspaces have a lot of important properties.
One property is that the column space is orthogonal to the left nullspace and the row space is orthogonal to the nullspace. This is relatively easy to show. The following equation is only satisfied by vectors in the nullspace.
\[ \textbf{A}x = 0\]Recall that the dot product, also called the inner product, or two orthogonal vectors is 1. From this we immediately see that the equation above shows that the column space of \(\textbf{A}\) and the nullspace of \(\textbf{A}^{T}\) must be orthogonal. Using a different equation, the same fact emerges for the row space of \(\textbf{A}\) and the nullspace of \(\textbf{A}\).
\[ \textbf{A}^{T}x = 0\]Another property of the fundamental subspaces is that the dimension of the column space and the null space adds to the number of columns. Likewise, the dimension of the row space and the dimension of the left nullspace adds up to the number of rows. Writing this in math:
Given an \(m\times n\) matrix \(\textbf{A}\), \[ \dim{(C(\textbf{A}))} + \dim{(C(\textbf{A}))} = n\] and \[ \dim{(R(\textbf{A}))} + \dim{(N(\textbf{A}^{T}))} = m\]
This starts to make sense when we look at rank of a matrix. The rank of a matrix is really the number of pivot columns we have in echelon form after doing Gauss-Jordan elimination. From our knowledge of elimation, we know that the number of pivot columns and the number of free columns adds up to the total number of columns in a matrix. These pivot columns are linearly independent and give us the basis for the column space of that matrix. The remaining columns contribute to the nullspace of that matrix. We can apply this same logic to the row space and left nullspace.
An algorithm that can be used to solve systems of linear equations and find the inverse of any invertible matrix. In doing this process, we can get elementary and permutation matrices.
Using the elementary row operations, we can get a matrix in echelon form and then perform back substitution.
There are three different types of elementary matrices. One for row exchange, row multiplication, and row addition. More details here. When multiplying elementary matrices, they usually go on the left.
\[ \textbf{E}\textbf{A} \]Permutation matrices, \(\textbf{P}\), have the property that
\[ \textbf{P}^{k} = \textbf{I} \] for some power \(k\)Elementary permutation matrices \(\textbf{E}_{p}\) have that
\[ \textbf{E}_{p} = \textbf{E}_{p}^{T} \]Row pictures and column pictures.
Row pictures make use of analyzing the rows, often as equations, whereas column pictures utilize the vectors.
Linear algebra has a lot of applications. Some of these applications happen to be in natural sciences such as chemistry. Balancing chemical equations is in essence just solving a system of linear equations which means that linear algebra can be applied rather smoothly.
This includes projections onto vectors and projections onto subspaces like the column space.
The projection matrix \(\textbf{P}\) is shown as follows: \[ \textbf{A}\hat{x} = \textbf{P}b = \textrm{proj}_{\textbf{A}}b \] \[ \textbf{P} = \textbf{A}(\textbf{A}^{T}\textbf{A})^{-1}\textbf{A}^{T} \]
To find this formula, we use an important equation that is named the normal equation.
\[ \textbf{A}^{T}(b - \textbf{A}\hat{x}) = 0 \]With this equation, \(\hat{x}\) gives the combination of \(\textbf{A}\) that yields a vector that ends at the tail of the error vector, \(b - \textbf{A}\hat{x}\).
There are two main properties that projection matrices have. The first is that they are symmetric. In other words, \(\textbf{P} = \textbf{P}^{T}\).
\[ (\textbf{A}(\textbf{A}^{T}\textbf{A})^{-1}\textbf{A}^{T})^{T} = \textbf{A}(\textbf{A}^{T}\textbf{A})^{-1}\textbf{A}^{T} \]The next property is that projection matrices are idempotent.
\[ \textbf{P}^{2} = \textbf{P} \]This leads to that fact that \(\textbf{P}^{k} = \textbf{P}\) for all \(k \in \mathbb{N}\)
Recall that the dot product of any two orthogonal vectors is equal to 1. Orthonormal vectors are simply just orthogonal vectors that have a magnitude of 1.
These are square matrices whose columns are orthonormal. It is important to note the disctinction between orthogonal matrices and matrices with orthonormal columns. They are not the same.
Examples: \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}\[ \frac{1}{2}\begin{bmatrix} 2 & 1 \\ 2 & -2 \\ 1 & 2 \end{bmatrix} \]
With these examples, we can see that the first and second are square matrices. Therefore, they are considered orthogonal matrices. The third example indeed has orthonormal columns, however it is not an orthogonal matrix due to the fact that it is rectangular and not square.
A key fact for a matrix with orthonormal columns \(\textbf{Q}\) is \[ \textbf{Q}^{T}\textbf{Q} = \textbf{I} \] and following from that is \[ \textbf{Q}^{T} = \textbf{Q}^{-1} \]
Every permutation matrix is orthogonal.
Going back to projections, when we project onto a matrix with orthonormal basis, we get \[ \textbf{P} = \textbf{Q}(\textbf{Q}^{T}\textbf{Q})^{-1}\textbf{Q}^{T} = \textbf{Q}\textbf{Q}^{T} \] Now, looking at orthonormal vectors, we see that \[ \textbf{P} = \textbf{I} \] Why is this? It is because since we have an orthogonal matrix, all of the columns are independent. With the matrix being square, the column space of the matrix takes up the whole entire vector space \( \mathbb{R}^{n} \).
This idea links directly to the previous topic of orthogonal matrices and matrices with orthonormal columns. Gram-Schmidt is a process used to take a matrix with linearly independent columns and make them orthonormal. This consists of two steps. First, we must make the columns orthogonal and then we must multiply by some appropriate multiple to have the magnitude equate to 1.
What we will do is take a matrix \(\textbf{A} = \begin{bmatrix} \vdots & \vdots & \vdots \\ a_{1} & a_{2} & a_{3} \\ \vdots & \vdots & \vdots \end{bmatrix} \) with independent columns \(a_{1}\), \(a_{2}\), and \(a_{3}\) and transform it into a matrix \(\textbf{C} = \begin{bmatrix} \vdots & \vdots & \vdots \\ c_{1} & c_{2} & c_{3} \\ \vdots & \vdots & \vdots \end{bmatrix} \) that has orthonormal columns \(c_{1}\), \(c_{2}\), and \(c_{3}\).
First, we will leave our first vector as is. \[a_{1} = b_{1}\] Now we have to make \(a_{2}\) orthogonal to \(a_{1}\).
\[ b_{2} = a_{2} - \frac{a_{1}\cdot a_{2}}{||a_{1}||^{2}} a_{1} \]We will do the same for the third column vector. \[ b_{3} = a_{3} - \frac{a_{1}\cdot a_{3}}{||a_{1}||^{2}} a_{1} - \frac{a_{2}\cdot a_{3}}{||a_{2}||^{2}} a_{2} \]
More generally
\[ b_{n} = a_{n} - \sum_{j=1}^{n-1} \textrm{proj}_{a_{j}}(a_{n}) \] \[ b_{n} = a_{n} - (\textrm{proj}_{a_{1}}(a_{n}) + \textrm{proj}_{a_{2}}(a_{n}) + \cdots + \textrm{proj}_{a_{n-1}}(a_{n})) \]Now we have completed the intermediate step and have the matrix \(\textbf{B} = \begin{bmatrix} \vdots & \vdots & \vdots \\ b_{1} & b_{2} & b_{3} \\ \vdots & \vdots & \vdots \end{bmatrix} \) with orthogonal columns \(b_{1}\), \(b_{2}\), and \(b_{3}\). Once we have made the columns orthogonal, we need to have their lengths be equal to 1. To do this, we simply divide each of the vectors by its magnitude.
\[ c_{1} = \frac{b_{1}}{||b_{1}||} \qquad c_{2} = \frac{b_{2}}{||b_{2}||} \qquad c_{3} = \frac{b_{3}}{||b_{3}||}\]We'll investigate to see why exactly this works. The length of a vector \(v\) with components \(v_{1}, v_{2}, \ldots, v_{n}\) is
\[ ||v|| = \sqrt{v\cdot v} = \sqrt{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}} \]Now we will suppose that every component is divided by the length of the vector. We will call this new vector \(w\).
\[ w = \frac{v}{||v||}\]The length then becomes
\[ w = \sqrt{w_{1}^{2} + w_{2}^{2} + \cdots + w_{n}^{2}} \] \[ w = \sqrt{\left(\frac{v_{1}}{\sqrt{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}}\right)^{2} + \left(\frac{v_{2}}{\sqrt{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}}\right)^{2} + \cdots + \left(\frac{v_{n}}{\sqrt{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}}\right)^{2}} \] \[ w = \sqrt{\frac{v_{1}^{2}}{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}} + \frac{v_{2}^{2}}{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}} + \cdots + \frac{v_{n}^{2}}{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}} \] \[ w = \sqrt{\frac{1}{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}\Biggl(v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}\Biggr)} \] \[ w = \sqrt{1} = 1 \]That is how we normalize a vector. This computational proof shows how dividing a vector's components by its magnitude results in a new vector of magnitude of 1.
\[ v = \begin{bmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{bmatrix} \qquad \frac{v}{||v||} = \frac{1}{||v||}\begin{bmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{bmatrix} \qquad \frac{v}{||v||} = 1 \]The only vector that this does not work with is the zero vector
\[ \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \]That is the process of Gram-Schmidt. In summary, we first make the basis vectors of the space orthogonal by subtracting their projections. After that we normalize every vector. That leaves us with an orthonormal basis for the same space. Pretty cool!
Determinants can essentially be thought of as a test for invertibility. If the determinant of a matrix is 0, then that matrix is singular. Conversely, if the determinant of that matrix is not equal to 0, then that matrix is invertible. There are many determinant properties. They can all be shown using three main properties.
\[ \det{\textbf{I}} = 1 \]Row exchanges of two rows reverses the sign of the determinant.
\[ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{23} & a_{33} \end{vmatrix} = - \begin{vmatrix} a_{21} & a_{22} & a_{23} \\ a_{11} & a_{12} & a_{13} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \]We performed a row exchange on the first and second rows above.
The determinant is linear in each rows of a matrix. This property can be split into two parts.
\[ \begin{vmatrix} \alpha a & \alpha b \\ c & d \end{vmatrix} = \alpha \begin{vmatrix} a & b \\ c & d \end{vmatrix} \] \[ \begin{vmatrix} a & b \\ c + s & d + t \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a & b \\ s & t \end{vmatrix} \]These three properties alone can be used to find a lot of other interesting properties of the determinant as well as arrive at a general formula of the determinant.
The fourth property that we will go over states that if a square matrix \( \textbf{A} \) has two rows that are equal, then the determinant of \(\textbf{A}\) is 0. The key here is using the second property. Let's show this with a 2 by 2 matrix.
\[ \begin{vmatrix} a & b \\ a & b \end{vmatrix} \]According to the second property, if I exchange row 1 and row 2, then the sign of the determinant flips.
\[ \begin{vmatrix} a & b \\ a & b \end{vmatrix} = -\begin{vmatrix} a & b \\ a & b \end{vmatrix} \]When we do this notice that the matrix remains the same. The only number that is equal to its negative is 0, therefore the determinant must be 0. Please note that this property holds for any \(n\) by \(n\) matrix. It is not restricted to only 2 by 2 matrices. Moving onto the fifth property. It states that if we subtract a multiple of one row from another, the determinant of the matrix remains unchanged. We'll show this property again with a 2 by 2 matrix for simplicity.
We will take some multiple of the first row by multiplying it by some number \(l\) and subtract that multiple from the second row.
\[ \begin{vmatrix} a & b \\ c - la & d - lb \end{vmatrix} \]Using previous properties, we can simplify this to be
\[ \begin{vmatrix} a & b \\ c - la & d - lb \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} - \begin{vmatrix} a & b \\ la & lb \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} - l\begin{vmatrix} a & b \\ a & b \end{vmatrix} \]As we can see, the matrix with the \(l\) has two identifical rows and thus its determinant must be 0. So we are left off with
\[ \begin{vmatrix} a & b \\ c - la & d - lb \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} \]Again, this property was shown using a 2 by 2 matrix for simplicity but this property can be applied to any \(n\) by \(n\) matrix. Onto property six: a matrix with a row of zeros has a determinant of 0. This can very easily be shown with the third property. If we have a matrix that has a row of only zeros, then we can factor out a 0. When doing so, we see that the determinant must be equal to 0.
Example:
\[ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 0 & 0 & 0 \end{vmatrix} = 0 \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 0 & 0 & 0 \end{vmatrix} = 0 \]Alright. For the next property, we will suppose that we have an upper triangular matrix \(\textbf{U}\). The determinant of \(\textbf{U}\) is just plus or minus the product of the entries on the diagonal (the pivots).
\[ \begin{vmatrix} d_{1} & \cdots & * \\ 0 & \ddots & \vdots \\ 0 & 0 & d_{n} \end{vmatrix} = (d_{1})(d_{2})(d_{3})\cdots(d_{n}) \]Now why is this the case? Well, if we are given a upper triangular matrix with nonzero values in the diagonal, then we can perform elimation to get just a diagonal matrix. Remember that by property five, elimation does not change the determinant of a matrix. With that being said, we can then use property three to factor out all of the diagonal values and be left with the identity matrix which, by property one, has a determinant of 1.
\[ \begin{vmatrix} d_{1} & 0 & 0 & \cdots & 0 \\ 0 & d_{2} & 0 & \cdots & 0 \\ 0 & 0 & d_{3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & 0 \\ 0 & 0 & 0 & 0 & d_{n} \end{vmatrix} = (d_{1})(d_{2})(d_{3})\cdots(d_{n}) \begin{vmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix} = (d_{1})(d_{2})(d_{3})\cdots(d_{n}) \ \textbf{I} = (d_{1})(d_{2})(d_{3})\cdots(d_{n}) \]With this formula, we now essentially have a method of computing the determinant of any square matrix. Let's show this with a 2 by 2 matrix.
\[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ 0 & d - \frac{c}{a}b \end{vmatrix} = a\left(d-\frac{c}{a}b\right) = ad - bc \]The eighth property is one that we have already stated but is worth mentioning again. The determinant of a matrix is 0 if and only if that matrix is singular. This property can be shown directly from the previous properties. If the matrix is singular, then we must have a row of zeros. That then implies that the determinant of the matrix is zero by property six. When the matrix is invertible, performing elimation transforms it into an upper triangular matrix. By property seven, we have that the determinant is simply the product of the pivots (which are all nonzero).
Property nine says that the determinant of a product of matrices is the product of the determinants. In math:
Given two squares matrices \(\textbf{A}\) and \(\textbf{B}\)
\[ \det{(\textbf{A}\textbf{B})} = (\det{\textbf{A}})(\det{\textbf{B}})\]Following this property is a nice fact.
\[ \det{(\textbf{A}\textbf{A}^{-1})} = \det{\textbf{I}} = 1\] \[ \det{(\textbf{A}\textbf{A}^{-1})} = (\det{\textbf{A}})(\det{\textbf{A}^{-1}}) = 1 \] \[ \det{\textbf{A}^{-1}} = \frac{1}{\det{\textbf{A}}} \]Another fact is
\[ \det{(\textbf{A}^{2})} = (\det{\textbf{A}})^{2} \]And one more is
\[ \det{(2\textbf{A})} = 2^{n}\det{\textbf{A}} \]The tenth property is another important one.
\[ \det{\textbf{A}^{T}} = \det{\textbf{A}} \]This means that all of the properties that applied to the rows of a matrix can also be applied to the columns of a matrix as well.
The properties of the determinant gave us a method for solving the determinant of any square matrix. Using the third property, which says that the determinant is linear to each row of a matrix, we see
\[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & 0 \\ c & d \end{vmatrix} + \begin{vmatrix} 0 & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & 0 \\ c & 0 \end{vmatrix} + \begin{vmatrix} a & 0 \\ 0 & d \end{vmatrix} + \begin{vmatrix} 0 & b \\ c & 0 \end{vmatrix} + \begin{vmatrix} 0 & b \\ 0 & d \end{vmatrix} \]Now we are left with four determinants. The first and last matrix have a determinant of 0 for a number of reasons. Having a column of zeros immediately tells us that it is not invertible. We could also multiply along the diagonal since they are triangular and clearly see that we would still arrive at the same conclusion. Computing the other determinants by performing the necessary row exchanges and multiplying the pivots, we get
\[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & 0 \\ 0 & d \end{vmatrix} + \begin{vmatrix} 0 & b \\ c & 0 \end{vmatrix} = ad - bc \]For general 2 by 2 matrices, the formula for the determinant is pretty easy to remember. However, doing this process for matrices of higher dimension gets a bit tedious. The idea remains the same though. With a 3 by 3 matrix, we would split the first row into three different matrices and do the same for the remaining two.
\[ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} = \begin{vmatrix} a_{11} & 0 & 0 \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} + \begin{vmatrix} 0 & a_{12} & 0 \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \]Continuing this process, we would get \(3^{3} = 27\) terms. Majority of these terms will automatically have a 0 determinant. As we saw with the 2 by 2 example, if the matrix has at least two nonzero entries in the same column, then there must be some zero along the diagonal. Finally, once we remove the determinants that automatically resolve to 0, we are left with
\[ \begin{vmatrix} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33} \end{vmatrix} + \begin{vmatrix} a_{11} & 0 & 0 \\ 0 & 0 & a_{23} \\ 0 & a_{32} & 0 \end{vmatrix} + \begin{vmatrix} 0 & a_{12} & 0 \\ a_{21} & 0 & 0 \\ 0 & 0 & a_{33} \end{vmatrix} + \begin{vmatrix} 0 & a_{12} & 0 \\ 0 & 0 & a_{23} \\ a_{31} & 0 & 0 \end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13} \\ a_{21} & 0 & 0 \\ 0 & a_{32} & 0 \end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13} \\ 0 & a_{22} & 0 \\ a_{31} & 0 & 0 \end{vmatrix} \]Notice that all of the entries do not share a row or column with the other entries. What we essentially have here is the permutations. All of these determinants can be solved. Half of them require that we perform a row exchange and reverse the sign.
\[ \begin{vmatrix} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33} \end{vmatrix} - \begin{vmatrix} a_{11} & 0 & 0 \\ 0 & a_{32} & 0 \\ 0 & 0 & a_{23} \end{vmatrix} - \begin{vmatrix} a_{21} & 0 & 0 \\ 0 & a_{12} & 0 \\ 0 & 0 & a_{33} \end{vmatrix} + \begin{vmatrix} a_{31} & 0 & 0 \\ 0 & a_{12} & 0 \\ 0 & 0 & a_{23} \end{vmatrix} - \begin{vmatrix} a_{21} & 0 & 0 \\ 0 & a_{32} & 0 \\ 0 & 0 & a_{13} \end{vmatrix} + \begin{vmatrix} a_{31} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{13} \end{vmatrix} = a_{11}a_{22}a_{33} - a_{11}a_{32}a_{23} - a_{21}a_{12}a_{33} + a_{31}a_{12}a_{23} + a_{21}a_{32}a_{13} - a_{31}a_{22}a_{13} \]We have now shown this process done on and 2 by 2 matrix as well as a 3 by 3 matrix. It is now time to write down the formula for a general \(n\) by \(n\) matrix. Again, notice that the columns of the three entries are permutations of the number of columns, \(n\). For the formula we arrive at the following:
\[ |\textbf{A}| = \sum \pm a_{1\alpha} a_{2\beta} a_{3\gamma} \ldots a_{n\omega} \] where \((\alpha, \beta, \gamma, \ldots, \omega ) = \textrm{permutations of } (1, 2, 3, \ldots, n) \)Remember that 1) there will \(n!\) terms because we are dealing with permutations and 2) that the sign of each term can either be plus or minus depending on how many row exchanges were needed to make the matrix diagonal.
Recall the formula that we got for the determinant of a 3 by 3 matrix.
\[ a_{11}a_{22}a_{33} - a_{11}a_{32}a_{23} - a_{21}a_{12}a_{33} + a_{31}a_{12}a_{23} + a_{21}a_{32}a_{13} - a_{31}a_{22}a_{13} \]This formula leads us onto the idea of cofactors. What we will do is factor out the entry from the first row from every two terms.
\[ a_{11}(a_{22}a_{33} - a_{32}a_{23}) + a_{12}(-a_{21}a_{33} + a_{31}a_{23}) + a_{13}(a_{21}a_{32} - a_{31}a_{22}) \]Looking at a previous picture we can start to see the significance of these numbers. We will start with the first term \(a_{11}(a_{22}a_{33} - a_{32}a_{23})\).
\[ \begin{vmatrix} a_{11} & 0 & 0 \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{vmatrix} \]The cofactor of \(a_{11}\) is \(a_{22}a_{33} - a_{32}a_{23}\) which is just the determinant of the 2 by 2 matrix that is leftover if the first row and column are excluded. This pattern mostly holds true for the other terms. Looking at the second term \(a_{12}(-a_{21}a_{33} + a_{31}a_{23})\), the cofactor of \(a_{12}\) is \(a_{31}a_{23} - a_{21}a_{33}\).
\[ \begin{vmatrix} 0 & a_{12} & 0 \\ a_{21} & 0 & a_{23} \\ a_{31} & 0 & a_{33} \end{vmatrix} \]Looking at the matrix, it looks like somethings off. From our previous logic, we expected to see that the cofactor would be the determinant of the remaining 2 by 2 matrix. From our formula that should be \(a_{21}a_{33} - a_{23}a_{31}\). Instead we got \(a_{31}a_{23} - a_{12}a_{33}\). The signs are reversed. Thinking back to our properties, this is because we need to perform row exchanges and consequently change the sign. In general, to determine the sign of the cofactor of \(a_{ij}\), we add \(i + j\) and if it is even, then the sign is plus and if its is odd, then the sign is minus. This sign is always incorporated into the cofactor.
Cofactor Formula (for row \(i\))
\[ |\textbf{A}| = \sum_{j = 1}^{n} a_{ij}C_{ij} = a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in} \] where \(C_{pq}\) is the cofactor of \(a_{pq}\)There we go! We now have three formulas for computing the determinant of a square matrix: the pivot formula, the general formula, and the cofactor formula. The pivot formula was not mentioned exclusively, but it is just reducing the matrix down into row echelon form and multiplying along the main diagonal (which should be the pivots if the matrix is not singular).
Now that we know the formulas for the determinant, we can apply them to problems that we had prior.
Cramer's rule, also known as the determinant method, is another way of solving \(\textbf{A}x = b\). It utilizes the alternative way of finding the inverse of a matrix \(\textbf{A}\) with its determinant and cofactors. It uses algebra rather than an algorithm like elimation. With a square invertible matrix \(\textbf{A}\), solving \(\textbf{A}x = b\) becomes a problem of computing \(n+1\) determinants.
We will start off with \(\textbf{A}x = b\).
\[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} x_{1} \\ \vdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} b_{1} \\ \vdots \\ b_{n} \end{bmatrix} \]This is the key:
\[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} x_{1} & 0 & 0 \\ x_{2} & 1 & 0 \\ x_{3} & 0 & 1 \end{bmatrix} = \begin{bmatrix} b_{1} & a_{12} & a_{13} \\ b_{2} & a_{22} & a_{23} \\ b_{3} & a_{32} & a_{33} \end{bmatrix} \]Notice that now when we take the determinant of both sides, we get
\[ \det{(\textbf{A}}) (x_{1}) = \det{\textbf{B}_{1}} \] \[ x_{1} = \frac{\det{\textbf{B}_{1}}}{\det{\textbf{A}}} \]We can get a similar formula for \(x_{2}, x_{3}, \ldots \). If we would like to solve for \(x_{2}\) for example, we would need to take the identity matrix and replace the second column with the column vector \(x\).
\[ \begin{vmatrix} 1 & x_{1} & 0 \\ 0 & x_{2} & 0 \\ 0 & x_{3} & 1 \end{vmatrix} = x_{2} \]Changing this matrix changes the matrix on the right hand side as well.
In general,
\[ \textbf{B}_{j} = \textbf{A} \textrm{ with column \(j\) replaced with \(b\)} \]When the right side is a column of the identity matrix, the determinant of each matrix \(\textbf{B}_{j}\) in Cramer's rule is a cofactor.
\[ \begin{vmatrix} 1 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & 1 & a_{13} \\ a_{21} & 0 & a_{23} \\ a_{31} & 0 & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & a_{12} & 1 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & 0 \end{vmatrix} \] \[ \begin{vmatrix} 0 & a_{12} & a_{13} \\ 1 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & 0 & a_{13} \\ a_{21} & 1 & a_{23} \\ a_{31} & 0 & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & 1 \\ a_{31} & a_{32} & 0 \end{vmatrix} \] \[ \begin{vmatrix} 0 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 1 & a_{32} & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & 0 & a_{13} \\ a_{21} & 0 & a_{23} \\ a_{31} & 1 & a_{33} \end{vmatrix} \qquad \begin{vmatrix} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & 1 \end{vmatrix} \]These are just the 3 by 3 cases, but this holds true for \(n\) by \(n\). With this, we can now solve for the columns of \(\textbf{A}^{-1}\) using Cramer's rule because \(\textbf{A}\textbf{A}^{1} = \textbf{I}\).
For clarification, we will solve \(\textbf{A}\textbf{A}^{-1} = \textbf{I}\) (the first column) for \(n=3\). The overall problem can be split into three different subproblems.
\[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \qquad \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \qquad \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} z_{1} \\ z_{2} \\ z_{3} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \] where \(\textbf{A}^{-1} = \begin{bmatrix} x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \\ x_{3} & y_{3} & z_{3} \end{bmatrix} \)However, we are only interested in the first one since we only want the first column of \(\textbf{A}^{-1}\)
\[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \] \[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} x_{1} & 0 & 0\\ x_{2} & 1 & 0 \\ x_{3} & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{bmatrix} \]Taking the determinant of both sides
\[ x_{1} = \frac{\det{\textbf{B}_{1}}}{\det{\textbf{A}}} = \frac{C_{11}}{\det{\textbf{A}}} \] where \(C_{11}\) is the cofactor of \(a_{11}\)Doing this for \(x_{2}\) and \(x_{3}\)
\[ \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} 1 & x_{1} & 0 \\ 0 & x_{2} & 0 \\ 0 & x_{3} & 1 \end{bmatrix} = \begin{bmatrix} a_{11} & 1 & a_{13} \\ a_{21} & 0 & a_{23} \\ a_{31} & 0 & a_{33} \end{bmatrix} \qquad\qquad \begin{bmatrix} & & \\ & \textbf{A} & \\ & & \end{bmatrix} \begin{bmatrix} 1 & 0 & x_{1} \\ 0 & 1 & x_{2} \\ 0 & 0 & x_{3} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & 1 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & 0 \end{bmatrix} \] \[ x_{2} = \frac{\det{\textbf{B}_{2}}}{\det{\textbf{A}}} = \frac{C_{12}}{\det{\textbf{A}}} \qquad\qquad x_{3} = \frac{\det{\textbf{B}_{3}}}{\det{\textbf{A}}} = \frac{C_{13}}{\det{\textbf{A}}} \]There is a pattern forming here. With Cramer's rule, we get the next two theorems.
\[ (\textbf{A}^{-1})_{ij} = \frac{C_{ji}}{|\textbf{A}|} \] where \(C_{ji}\) is the cofactor of \(a_{ji}\) \[ \textbf{A}^{-1} = \frac{\textbf{C}^{T}}{|\textbf{A}|}\] where \(\textbf{C}\) is the matrix of cofactors for the entries of \(\textbf{A}\)Now we have a formula for computing the inverse of a square invertible matrix using determinants and cofactors.
Let's look at the 2 by 2 case.
\[ \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \]The formula also translates into
\[ \textbf{A}\textbf{C}^{T} = (\det{\textbf{A}}) \ \textbf{I} \]We will try to verify this equation.
\[ \textbf{A}\textbf{C}^{T} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} C_{11} & C_{21} & \cdots & C_{n1} \\ C_{12} & C_{22} & \cdots & C_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ C_{1n} & C_{2n} & \cdots & C_{nn} \end{bmatrix} \]Computing the first entry of the product, we get the dot product of the first row of \(\textbf{A}\) and the first column of \(\textbf{C}^{T}\) which is
\[ a_{11}C_{11} + a_{12}C_{12} + \cdots + a_{1n}C_{1n} \]This is just the cofactor formula for the determinant of \(\textbf{A}\) which indicates that this is just that. If we continue on, we will see that we will always get the determinant of \(\textbf{A}\) along the main diagonal of the product.
\[ \begin{bmatrix} \det{\textbf{A}} & & & \\ & \det{\textbf{A}} & & \\ & & \ddots & \\ & & & \det{\textbf{A}} \end{bmatrix} \]The next step would be to figure out what lies above and below the diagonal.
Computing the entry for row two, column one of the product, we get the the dot product of the second row of \(\textbf{A}\) and the first column of \(\textbf{C}^{T}\).
\[ a_{21}C_{11} + a_{22}C_{12} + \cdots + a_{2n}C_{1n} \]This is simply the cofactor formula for some matrix. For this formula to yield the determinant of that matrix, the first row must be equal to the second row. Now, we know that if two rows of a matrix are identical, then that matrix is singular and as a result, the determinant is 0. If we go back to cofactors and look at this visually with the matrix
\[ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} = \begin{vmatrix} a_{21} & a_{22} & \cdots & a_{2n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} = 0 \]With that being said, all of the entries above and below the main diagonal must be 0.
\[ \begin{bmatrix} \det{\textbf{A}} & & & 0 \\ & \det{\textbf{A}} & & \\ & & \ddots & \\ 0 & & & \det{\textbf{A}} \end{bmatrix} = (\det{\textbf{A}}) \ \textbf{I} \]And just like that, we showed that the equation indeed holds up.
The determinant is a way to express volume. For instance, in \(\mathbb{R}^{3}\), the rows of a 3 by 3 matrix represent the sides of a parallelepiped. When the volume of this determinant is computed, it happens to be the volume of the parallelepied. When we multiply one of the sides of the determinant by any scalar, say 2, the volume of the paralellepiped should double. According to property three, the determinant is also scaled by 2. So that property holds up. With a little bit of checking, we can find that all of the other properties hold up as well. This is a pretty fascinating fact about the determinant.
\[ \textrm{Volume} = |\det{\textbf{A}}| \]The idea of determinants as volumes are also useful in calculus when looking at Jacobians.
The cross product is an additional application of the determinant. It is special for three dimensions. It is a vector that is orthogonal to two other vectors.
Given two vectors \(u = (u_{1}, u_{2}, u_{3})\) and \(v = (v_{1}, v_{2}, v_{3})\)
\[ ||u \times v|| = ||u|| \ ||v|| \sin{\theta} \] where \(\theta\) is the angle between \(u\) and \(v\)A mnemonic that is used for the cross product is
\[ u \times v = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{vmatrix} = (u_{2}v_{3} - u_{3}v_{2})\hat{i} + (u_{3}v_{1} - u_{1}v_{3})\hat{j} + (u_{1}v_{2} - u_{2}v_{1})\hat{k} \] where \(\hat{i}\), \(\hat{j}\), and \(\hat{k}\) are standard basis vectors.Using properties of the determinant, we see that \(u \times v = -(v \times u)\) because exchanging rows reverses the sign.
Related to the cross product is the triple product.
\[ (x\times y) \cdot z = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \end{vmatrix} \cdot z = \left[ (x_{2}y_{3} - x_{3}y_{2})\hat{i} + (x_{3}y_{1} - x_{1}y_{3})\hat{j} + (x_{1}y_{2} - x_{2}y_{1})\hat{k} \right] \cdot z = \begin{bmatrix} x_{2}y_{3} - x_{3}y_{2} \\ x_{3}y_{1} - x_{1}y_{3} \\ x_{1}y_{2} - x_{2}y_{1} \end{bmatrix} \cdot \begin{bmatrix} z_{1} \\ z_{2} \\ z_{3} \end{bmatrix} = z_{1}(x_{2}y_{3} - x_{3}y_{2}) + z_{2}(x_{3}y_{1} - x_{1}y_{3}) + z_{3}(x_{1}y_{2} - x_{2}y_{1}) \]Notice that this is just the cofactor formula. So
\[ (x\times y) \cdot z = \begin{vmatrix} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \\ z_{1} & z_{2} & z_{3} \end{vmatrix} \]As we can see, the triple product is just the determinant. Note that \(z\) can either be put in the first row or the last row.
\[ \textrm{Triple Product} = \textrm{Determinant} = \textrm{Volume} \]The area of a triangle can also be obtained using determinants. We know that the area of a rectangle is base times height. The area of a triangle is a half the base times height.
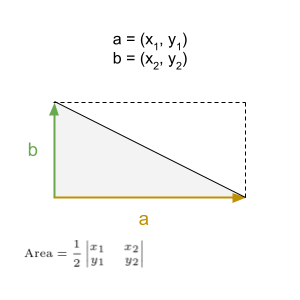\[ \textrm{Area of} \ \triangle = \frac{1}{2} \begin{vmatrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{vmatrix} \]