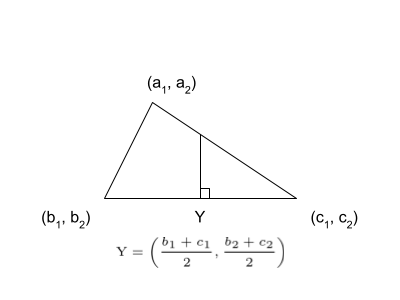This webpage is my collection of notes for Mr. Healey's geometry class.
If you enjoy anime, you might enjoy this.
- Notation
Here is some brief information on the topic of the notation used in geometry. The main figures that we work with are points, lines, line segments, rays, and angles. It is important to distinguish them between their measurements.
|
| Figure |
Measurement |
| Point |
\[ \rm A \] |
There is no measurement for points |
| Lines |
\[ \overleftrightarrow{\rm AB} \] |
There is no (finite) measurement for lines |
| Line segments |
\[ \overline{\rm AB} \] |
\[ \rm AB \] |
| Rays |
\[ \overrightarrow{\rm AB} \] |
There is no (finite) measurement for rays |
| Angles |
\[ \angle{\rm ABC}\] |
\[ m\angle{\rm ABC} \] |
| Triangles |
\[ \triangle{\rm ABC} \] |
There is no measurement for triangles |
| Arcs |
\[ \widehat{\rm ABC} \] |
\[ m\widehat{\rm ABC} \] |
One thing to note here is that figures can be congruent whereas measurements can be equal. For instance, if two line segments \( \overline{\rm AB} \) and \( \overline{\rm CD} \) are congruent, then their lengths, denoted \(\rm AB\) and \(\rm CD \), are equal. This is the definition of congruent segments.
\[ \overline{\rm AB} \cong \overline{\rm CD} \qquad \textrm{if, and only if} \qquad {\rm AB} = {\rm CD} \]
The same thing goes for angles. Rays and lines do not have finite lengths because they both go off indefinetly and for triangles, there is not one sole measurement that describes it.
Given a diagram, congruent sides are denoted with hash marks. Congruent angles are marked in a somewhat similar fashion but with arcs instead.
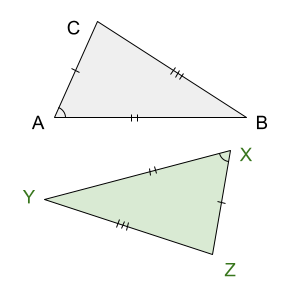\[ \triangle{\rm ABC} \cong \triangle{\rm XYZ} \]
- Two parallel lines cut by a transversal
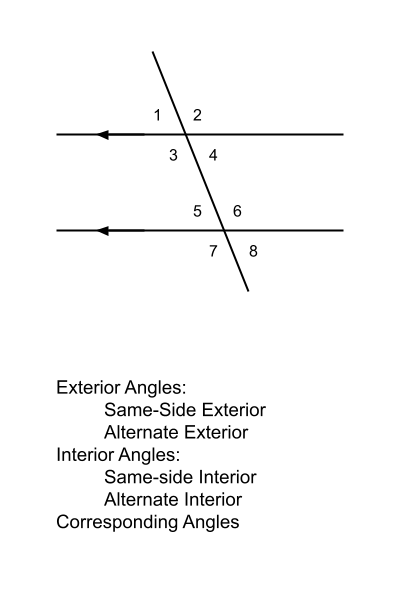
Alternate Exterior Angles Thereom
Same-side Interior Angles Postulate
Alternate Interior Angles Theorem
Corresponding Angles Theorem
- Two Column Proofs
What exactly are proofs? They are arguments that are used to prove statements.
Geometry has a close relationship to the history of proofs. Euclid was a geometer and logician, refered to by some as the "father of geometry". During the time of ancient Greek mathematicians, shapes were often used to prove different theorems. This basic idea of proofs still remains today. You must use axioms or postulates to build your argument. These are statements that are assumed to be true. The terms "axiom" and "postulate" have differed historically, however in modern day they are mostly interchangable. The term "postulate" is specific to geometry. They can be thought of as the building blocks of a proof.
The basic structure of a two column proof is as follows:
With proofs, you should always start with your hypothesis and end with your conclusion. Your hypothesis is synonymous to your "given". Your conclusion is simply what you sought out to prove.
| Statement |
Reason |
| (Hypothesis) |
Given |
| \[ \vdots \] |
\[ \vdots \] |
| (Conclusion) |
Q.E.D. |
Q.E.D. is an abbreviation for the latin phrase quod erat demonstrandum. This translates to "which was to be demonstrated."
Here are some of the theorems/postulates used in geometry:
- Reflexive property
\[ \overline{\rm AB} \cong \overline{\rm AB} \]
- Symmetric property
\[ \overline{\rm AB} \cong \overline{\rm BA} \]
- Definition of congruent segments
- Definition of congruent angles
- Corresponding parts of congruent triangles are congruent (CPCTC)
- Definition of a midpoint
\[ {\rm B} \ \textrm{is a midpoint of} \ \overline{\rm AC} \qquad \textrm{if, and only if} \qquad \overline{\rm AB} \cong \overline{\rm BC} \]
- Definition of angle bisection
- Definition of segment bisection
- Definition of angle trisection
- Definition of segment trisection
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- SSS (Side-Side-Side)
- HL (Hypotenuse-Leg)
This can be thought of as a special case of the SSS postulate. Given two right triangles with two congruent sides, we can use the pythagorean theorem to solve for the remaining side.
\[ a^{2} + b^{2} = c^{2} \]
The remaining side of one right triangle must be congruent to the remaining side of the other right triangle.
- Third angles theorem
- and many more...
- Area of a Circle Formula Derivation
In math, one thing that I dislike is purely memorizing formulas. I will try to demonstrate a slightly more intuitive way of deriving and understanding the formulas for a circle. This approach involves the essential idea of calculus—infinitesimals. The key fact that you will have to remember is that the irrational constant pi, denoted by lowercase Greek letter \(\pi\), is the ratio of a circle's circumference (perimeter) to its diameter (width). This is like the definition of pi.
\[ \pi = \frac{C}{D} \]
Immediately from this, we can solve for the circumference.
\[ C = \pi D \]
By definition, the radius of a circle is twice its diameter.
\[ 2r = D \]
Plugging this into the previous equation, we see that the circumference of a circle in terms of its radius is
\[ C = 2\pi r \]
Now, how can we obtain the circle's area? First we will start with approximations. Notice that if we divided the circle into segments, we can approximate the area of each of them by treating them as triangles.
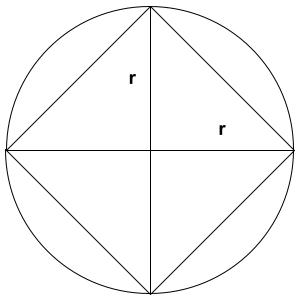
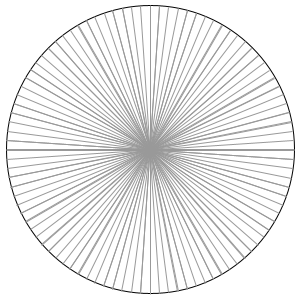
If we split the circle into four segments, the area of each of these segments is given by \(\frac{1}{2} r^{2} \). If we add these areas, we will get an approximation for the area of the entire circle.
\[ \textrm{Approximation } = 4 \left( \frac{1}{2}r^{2} \right) = 2r^{2} \]
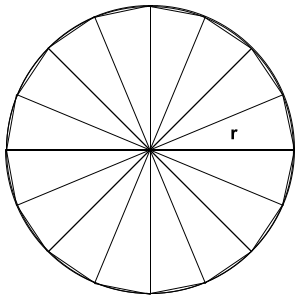
Obviously this is not such a great approximation. How do we make our approximation more accurate. To do this, we will divide the circle into more segments. When we do this, the associated error of each segment's approximation is reduced.
Now here comes the calculus! If we continue to split the circle into more and more segments, the error will continue to get smaller and smaller to the point where it is negligible (so small that we can consider it insignificant). When we do this we are left with a lot of very small triangles. These small triangles are called infinitesimals. By calclating the sum of their areas, we arrive at the area of the entire circle. To find this area, we use a the following pictorial representation.
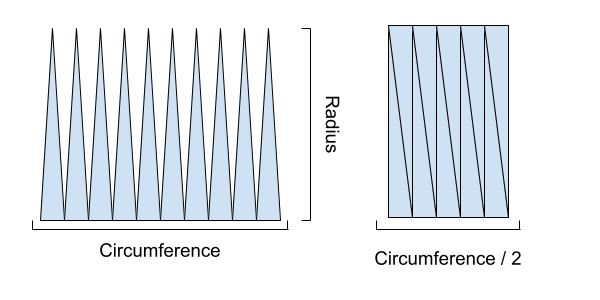
Figure not drawn to scale
Notice that all of these triangles are congruent. If we have two congruent triangles, we can combine them into a single rectangle as we did above. With this fact, we can create one large rectangle that represents the area of the entire circle. Of course the area of a rectangle is simply length times width.
\[ \textrm{Area of Rectangle} = L \times W \]
In this case, the length is half the circumference, \(\frac{1}{2}C\), and the width is the radius, \(r\). So we see that the area of the circle is
\[ \textrm{Area} = \frac{1}{2}C r \]
Using the previous formula for the circumference, we can perform a substition.
\[ \textrm{Area} = \frac{1}{2}2\pi r^{2} = \pi r^{2} \]
There we go!
\[ \textrm{Area of Circle} = \pi r^{2} \]
With the formulae for the area of a circle and its circumference, we can obtain formulae for the arc length and area of a sector.
- What is a Sector?
Sectors are portions of a fractions of a circle given by some angle \(\theta\). It is bounded by two radii and an arc of a circle.
Image Source: Wikipedia
- Arc length and Area of Sector Formula Derivation
Now we are onto arc length. The arc length measures a portion of the circumference of a circle. It is the length of an arc on a circle.
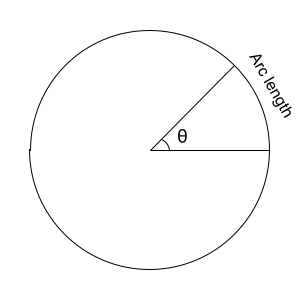
First, we must determine the ratio of the sector given by \(\theta\) to the whole circle. It will be a fraction. For this, we will need to use the fact that a full circle is 360° or \(2\pi\) radians.
When \(\theta\) is measured in radians, the fraction will
\[ \frac{\theta}{2\pi} \]
How does this work? Let's say \(\theta = \pi \). Calculating the fraction, we get
\[ \frac{\theta}{2\pi} = \frac{\pi}{2\pi} = \frac{1}{2} \]
This makes perfect sense. Half a circle is \(\pi\) radians. This implies that the arc length, denoted by \(s\), will be half of the circumference as well.
\[ s = \frac{1}{2}C \]
This is essentially the formula for arc length. We multiply the percentange of the circle by the circumference and we obtain the corresponding arc length.
\[ s = \frac{\theta}{2\pi}C \]
Remember that \(C = 2\pi r \)
\[ s = \frac{\theta}{2\pi}2\pi r = r\theta \]
Arc Length Formula:
The formula for the arc length of a circle is
\[ s = r\theta \]
Taking the same approach, we can calculate the area of sector. All we need is the ratio of the sector to the full circle and then we multiply that by the area of the full circle.
Area of Sector Formula:
\[ \textrm{Area of Sector} = \frac{\theta}{2\pi} \pi r^{2} = 2\pi \theta r \]
When \(\theta\) is not measured radians, but instead degrees, you must use a conversion factor.
\[ \frac{\pi}{180°} \]
- 03/01/2023 Notes
Definitions:
Exterior angle
Remote interior angle
Theorems:
- Triangle Sum Theorem — the sum of the measures of the interior angles of a triangle is 180 degrees.
- Exterior Angle Theorem — the measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
- Isoceles Triangle Theorem — if two sides of a traingle are congruent, the the two angles opposite the congruent sides are congruent.
- 03/03/2023 Notes
Theorems:
- Circumcenter Theroem — the perpendicular bisectors of the sides of a triangle intersect at a point that is equidistant from the vertices of the triangle. The point at which they intersect is called the circumcenter.
- Calcuating the Circumcenter of a Triangle
Check out the notes here.
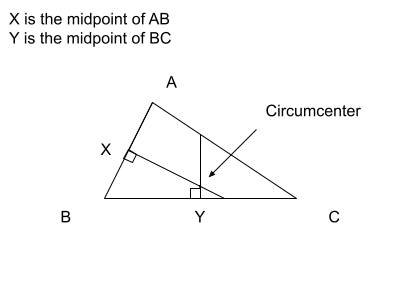
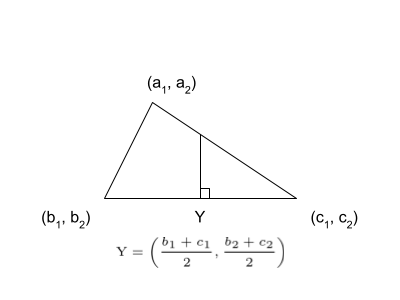
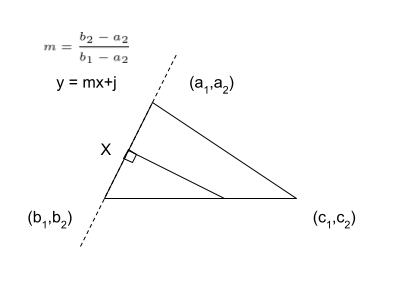
There is a more interactive visual that I created on Desmos.
- Formula Reference
|
Formula |
| Midpoint |
\( (\overline{x}, \overline{y}) = \left(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2} \right) \) |
| Slope |
\( m_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) |
| Perpendicular Slope |
\( m_{2} = -\frac{1}{m_{1}} = \frac{x_{1} - x_{2}}{y_{2} - y_{1}} \) |
| Slope-intercept Form |
\( y = mx + b \) |
| Point-slope Form |
\( y - y_{1} = m(x - x_{1}) \) |
| Perpendicular Bisector of \(\overline{\rm AB}\) where \({\rm A} = (x_{1}, y_{1})\) and \({\rm B} = (x_{2}, y_{2})\) |
\( \begin{align} y &= m_{2}(x - \overline{x}) + \overline{y} \\ &= \frac{x_{1} - x_{2}}{y_{2} - y_{1}}\left(x - \frac{x_{1} + x_{2}}{2} \right) + \frac{y_{1} + y_{2}}{2} \end{align} \) |
- Triangle Inequality Theorem
\[ |a+b| \leq |a| + |b| \]
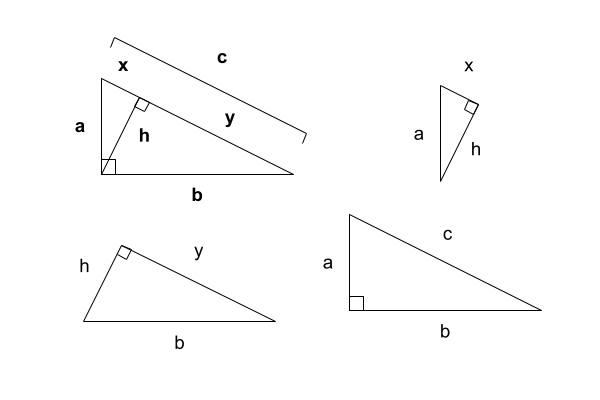
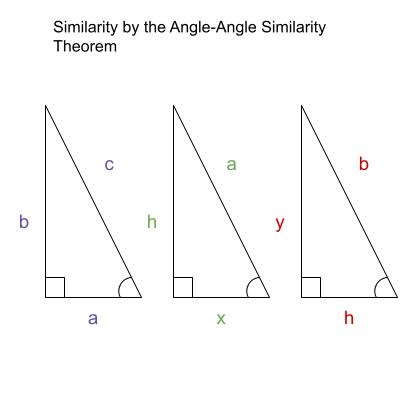
- The Four Ancient Triangle Centers: Triangle Centroid, Incenter, Circumcenter, and Orthocenter
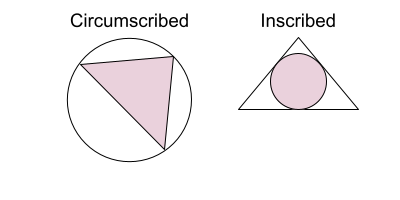
- Circumscribed vs. Inscribed
