The Jacobian can be used to change variables when integrating over double or triple integrals. It can be thought of as the scaling factor between one coordinate space and another.
\[ \frac{\partial (x, y)}{\partial (u, v)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix} = \frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\]Terms
The general solution is the solution that does not take the initial conditions (i.c.'s) into account. The actual solution is the solution that satisfies both the DE and the i.c.'s.
Implicit/Explicit solution
Slope/Direction fields
Euler's method — technique used to analyze a DE.
Seperable equations
\[ \frac{dx}{dt} = f(x)g(t) \] \[ \int \frac{1}{f(x)}dx = \int g(t)dt \]Second order linear homogenous DE
\[ Ay'' + By' + Cy = 0 \]Using leibniz's notation
\[ A\frac{d^{2}y}{dx^{2}} + B\frac{dy}{dx} + Cy = 0 \]For DEs of this type, the sum of two or more solutions is also a solution. We can also multiply each solution by a constant as well. In Differential Equations, this is called the superposition principle. This is much like taking linear combinations in linear algebra.
Given a general second order linear homogenous DE like the one above, suppose that \(g(x)\) is a solution.
\[ Ag'' + Bg' + Cg = 0\]Then \(kg(x)\) is also a solution for any constant \(k\).
Let's check this.
\[ Akg'' + Bkg' + Ckg \] \[ k(Ag'' + Bg' + Cg) \]We see that \(Ag'' + Bg' + Cg\) is a solution, so its value must be equal to 0. Therefore
\[ k(Ag'' + Bg' + Cg) = 0 \]and thus, \(kg(x)\) is indeed a solution to the equation.
Given a general second order linear homogenous DE like the one above, suppose that \(g(x)\) and \(h(x)\) are solutions.
Then
\[ Ag'' + Bg' + Cg = 0 \]and
\[ Ah'' + Bh' + Ch = 0 \]An important fact is that if \(g(x)\) and \(h(x)\) are solutions to this equation, then \(g(x) + h(x)\) is too.
Let's verify.
\[ A(g + h)'' + B(g + h)' + C(g + h) \]Using the fact that the derivative of a sum is equal to the sum of their derivatives
\[ A(g'' + h'') + B(g' + h') + C(g + h) \] \[ Ag'' + Ah'' + Bg' + Bh' + Cg + Ch \] \[ (Ag'' + Bg' + Cg) + (Ah'' + Bh' + Ch) \]Knowing that \(g(x)\) and \(h(x)\) are solutions
\[ (Ag'' + Bg' + Cg) + (Ah'' + Bh' + Ch) = 0 \]and just like that we showed that the sum of two solutions is also a solution.
Example:
\[ y'' + 5y' + 6y = 0 \]For these problems, we often assume that our solution will be in the form \( y = e^{rx} \). Using this, we can get the derivatives.
| Derivative \(n\) | Function \(f^{(n)}(x)\) |
|---|---|
| 0 | \(e^{rx}\) |
| 1 | \(re^{rx}\) |
| 2 | \(r^{2}e^{rx}\) |
Plugging in the above values, we get
\[ r^{2}e^{rx} + 5re^{rx} + 6e^{rx} = e^r{x}( r^{2} + 5r + 6 ) = 0 \]Factoring the polynomial
\[ e^{rx}( r^{2} + 5r + 6 ) = e^{rx}(r+3)(r+2) = 0 \]We call \(r^{2} + 5r + 6 = 0\) the characteristic equation as it gives the solutions to this DE.
Solving the equation using simple algebra, we get two solutions to the polynomial.
\[ r = -3 \qquad r = -2 \]This means that the solutions to the DE are
\[ y = e^{-3x} \qquad y = 3^{-2x} \]Recall that the linear combinations of solutions to second order linear homogeneous DEs are also solutions. This fact stems from the fact that differentiation is a linear operation.
Therefore the general solution is
\[ y = c_{1}e^{-3x} + c_{2}e^{-2x} \] for real numbers \(c_{1}\) and \(c_{2}\).To get values for \(c_{1}\) and \(c_{2}\) for the actual solution, we need initial conditions. The i.c.'s for second order linear homogeneous DEs can be a point in terms of \(y\) and a point in terms of \(y'\).
Let us suppose that the i.c.'s for this problem are
\[ y(0) = 2 \qquad y'(0) = 3 \]All we have to do is plug these values into our equation and solve the system.
\[ y = c_{1}e^{-3x} + c_{2}e^{-2x} \] \[ y' = -3c_{1}e^{-3x} + -2c_{2}e^{-2x} \]\[ 2 = c_{1} + c_{2} \] \[ 3 = -3c_{1} + -2c_{2} \]
To solve this system, we can either use standard techniques from basic algebra or utilize linear algebra. I will do the latter.
\[ \begin{bmatrix} 1 & 1 \\ -3 & -2 \end{bmatrix} \begin{bmatrix} c_{1} \\ c_{2} \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \] \[ \begin{bmatrix} 1 & 1 \\ -3 & -2 \end{bmatrix} \begin{bmatrix} c_{1} \\ c_{2} \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \] \[ \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} c_{1} \\ c_{2} \end{bmatrix} = \begin{bmatrix} 2 \\ 9 \end{bmatrix} \] \[ \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} c_{1} \\ c_{2} \end{bmatrix} = \begin{bmatrix} -7 \\ 9 \end{bmatrix} \]and with the matrix in RREF, we finally see that
\[ c_{1} = -7 \qquad c_{2} = 9 \]which means that actual solution corresponding to these initial conditions is
\[ y = 9e^{-2x} - 7e^{-3x} \]Classifying Differential Equations
Steady state
Stability
I briefly explained the process and demonstrated an example on the linear algebra page.
\(\vec{u}\) is a unit vector.
\[ \vec{u} = \begin{bmatrix} u_{1} \\ u_{2} \\ \vdots \\ u_{n} \end{bmatrix} \] \[ D_{\vec{u}}f(x_{1}, x_{2}, \ldots, x_{n}) = \lim_{h\to 0} \frac{f(x_{1} + u_{1}h, x_{2} + u_{2}h, \ldots, x_{n} + u_{n}h) - f(x_{1}, x_{2}, \ldots, x_{n})}{h} \]Here is the three dimensional case. The vector \(\vec{u}\) will be \(\mathbb{R}^{2}\) and define a function \(g\) of two variables, \(x\) and \(y\).
Let \(\vec{u} = \begin{bmatrix} a \\ b \end{bmatrix} \)
\(\vec{u}\) is on the \(xy\)-coordinate plane.
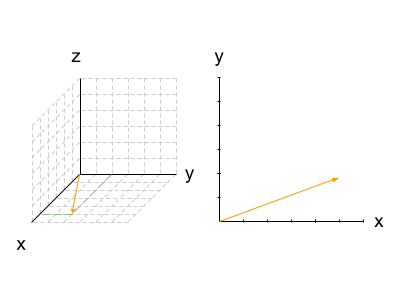 \[ D_{\vec{u}}g(x, y) = \lim_{h\to 0} \frac{g(x + ah, y + bh) - g(x, y)}{h} \]
\[ D_{\vec{u}}g(x, y) = \lim_{h\to 0} \frac{g(x + ah, y + bh) - g(x, y)}{h} \]
\[ D_{\vec{u}}g(x, y) = g_{x}(x, y)a + g_{y}(x, y)b \]
Gradient, also called the gradient vector
\[ \nabla g = \begin{bmatrix} g_{x}(x, y) \\ g_{y}(x, y) \end{bmatrix} \]\[ D_{\vec{u}}g(x, y) = \nabla g \cdot \vec{u} \]
Here is an application of the Schwarz inequality.
\[ D_{\vec{u}}g(x, y) = \nabla g \cdot \vec{u} \] \[ = ||\nabla g|| \ ||\vec{u}|| \cos\theta \]Recall that \(\vec{u}\) is a unit vector. This means
\[ ||\vec{u}|| = 1 \] \[ = ||\nabla g|| \cos\theta \]Now with \(\cos\theta\), we know that its values are always between -1 and 1.
\[ -1 \leq \cos\theta \leq 1 \] \[ |\cos\theta| \leq 1 \]Therefore,
\[ D_{\vec{u}}g(x, y) \leq ||\nabla g|| \]